Revue d'Evidence-Based Medicine
Comment analyser des mesures répétées ?
Ce numéro de Minerva commente une étude randomisée contrôlée évaluant l’effet de la restriction de sommeil sur la qualité du sommeil (1). Les investigateurs ont utilisé, entre autres, deux échelles, le score PSQI et le score ISI, pour mesurer de manière objective la qualité du sommeil tant dans le groupe intervention que dans le groupe témoin (2).
Falloon K, Elley CR, Fernando A 3rd, et al. Simplified sleep restriction for insomnia in general practice: a randomized controlled trial. Br J Gen Pract 2015;65:e508-15.
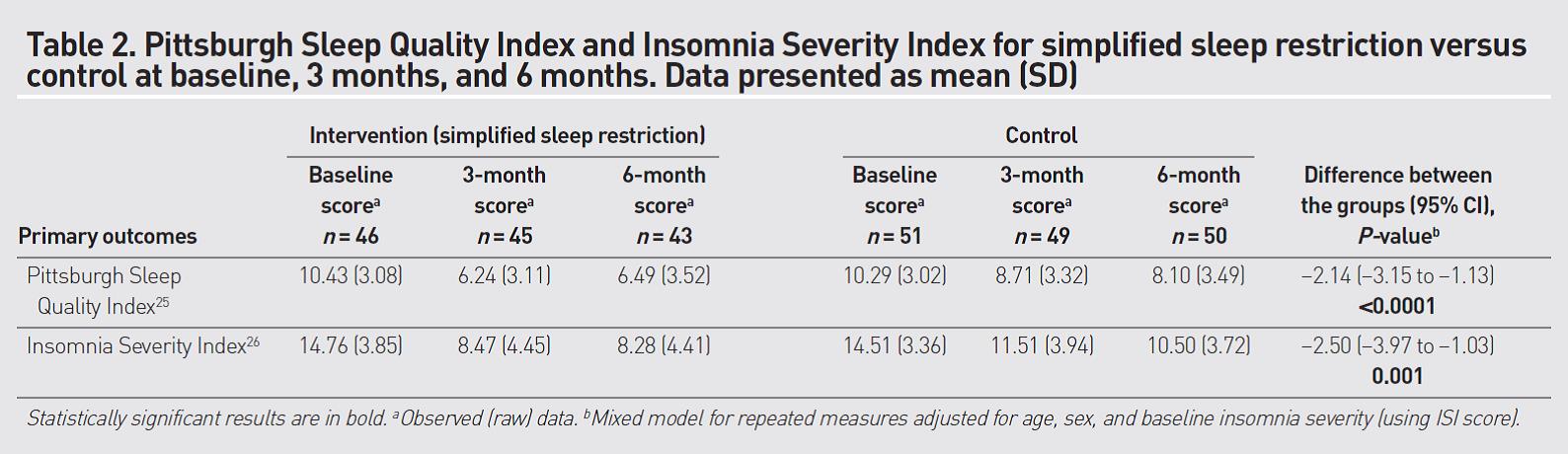
Pour chaque patient, les chercheurs ont effectué trois mesures : à la randomisation, après trois mois et après six mois de suivi. Comme les scores PSQI et ISI initiaux différaient peu entre les deux groupes, nous pourrions, en principe, utiliser la différence entre les deux groupes du score différentiel moyen (le score après suivi au cours du sixième mois moins le score de début d’étude) pour déterminer l’efficacité du traitement (3). Pour le score PSQI, nous aurions alors une diminution de (6,49 – 10,43) – (8,10 – 10,29) = -1,75 points, et pour le score ISI, une diminution de (8,28 – 14,76) – (10,50 – 14,51) = -2,47 points. Dans le tableau 2 de l’article original, les investigateurs mentionnent pourtant une différence entre les deux groupes des scores PSQI et ISI de respectivement -2,14 points (avec IC à 95% de -3,15 à -1,13) et de -2,50 points (avec IC à 95% de -3,97 à -1,03). Nous voyons donc, surtout pour le score PSQI, une différence de près d’un demi-point. Comment expliquer cette différence ?
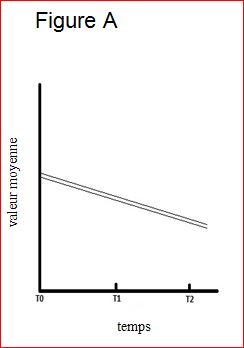
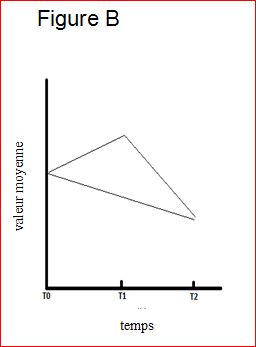
Si nous mesurons un critère de jugement à différents moments, deux mesures chez une même personne seront plus semblables que deux mesures chez des personnes différentes. Il existe donc une certaine corrélation entre les mesures répétées chez une même personne (4). Du fait de cette corrélation, l’effet moyen d’un traitement peut varier dans un groupe de traitement selon le moment de la mesure. En outre, l’effet relatif entre un groupe intervention et un groupe témoin peut varier selon le moment de la mesure du fait d’une interaction entre l’ampleur de l’effet du traitement (intervention versus contrôle) et le moment de la mesure. Les figures ci-dessous illustrent séparément les valeurs moyennes d’un critère de jugement en fonction du moment de mesure pour le groupe intervention et pour le groupe témoin. La figure A montre dans les deux groupes de traitement une diminution similaire des valeurs moyennes du critère de jugement aux temps T1 et T2. Il n’y a donc pas d’interaction entre l’ampleur de l’effet et le moment de la mesure. Comme les lignes sont quasi superposées, il n’y a pas de différence quant à l’effet entre les deux groupes de traitement. La figure B ne montre pas de différence quant aux valeurs moyennes du critère de jugement entre les deux groupes de traitement aux temps 0 et 2, mais bien au temps 1. Imaginons maintenant que nous ne tenions compte que du temps 0 et du temps 2, notre conclusion serait qu’il n’y a pas de différence quant à l’effet entre le groupe intervention et le groupe témoin. Nous voyons cependant une grande différence quant à l’ampleur de l’effet entre, d’une part, le temps 0 et le temps 2 et, d’autre part, le temps 1. Il existe donc bien une interaction entre l’ampleur de l’effet et le moment de la mesure. Si on en tient compte, il y aura probablement bien une différence statistiquement significative entre les deux groupes de traitement quant à l’effet.
La correction effectuée dans le but de tenir compte de la corrélation de mesures successives pour chaque participant dans un groupe de traitement et pour savoir s’il existe une interaction entre l’ampleur de l’effet et le moment de la mesure, peut se faire en utilisant une ANOVA sur mesures répétées. L’ANOVA (analysis of variance - analyse de la variance) est effectuée pour comparer la moyenne d’un critère de jugement continu entre au moins trois groupes (« traitement ») indépendants (5). Une ANOVA sur mesures répétées compare la moyenne d’un critère de jugement continu (intervention versus contrôle) à différents moments de mesure et cherche à déterminer l’existence d’une interaction entre l’ampleur de l’effet et le moment de la mesure. Cette méthode prévoit cependant des conditions très strictes que l’étude ne peut pas toujours remplir dans la réalité. Les mesures doivent être prises au même moment chez tous les participants, et les données manquantes ne sont pas autorisées. En outre, cette méthode ne permet pas de calculer l’ampleur de l’effet. C’est pourquoi un modèle linéaire à effets mixtes est souvent utilisé. Il s’agit en fait d’une analyse par régression complexe qui permet de calculer l’ampleur de l’effet en tenant compte de la variation des mesures avec le temps chez un même participant et de l’éventuelle interaction entre cette variation et l’ampleur de l’effet. L’avantage de cette méthode, tout comme l’ANCOVA (3), est de pouvoir aussi tenir compte d’autres facteurs de confusion. Ses désavantages sont sa complexité, la puissance de calcul requise et la nécessité d’un logiciel optimalisé (6).
Dans notre exemple, le modèle à effets mixtes a été choisi de manière à pouvoir calculer l’ampleur de l’effet de la restriction de sommeil comparée au contrôle en tenant compte de la corrélation des mesures chez un même participant, de l’interaction d’une différence de l’ampleur de l’effet entre différents moments de mesure ainsi que des facteurs de confusion tels que l’âge, le sexe et le degré d’insomnie au départ. Le fait que ce n’est que pour le score PSQI qu’il y avait une différence dans l’ampleur de l’effet quand on avait recours à un modèle à effets mixtes suggère que l’effet thérapeutique différait selon le moment de mesure uniquement pour ce score PSQI mais non pour le score ISI.
Conclusion
Lorsque le critère de jugement pour tous les participants d’une étude sont mesurés à différents moments, une méthode d’analyse qui tient compte du fait que les mesures ne sont pas indépendantes les unes des autres et que l’effet du traitement peut être différent en fonction du moment où la mesure est effectuée doit être utilisée. Il est alors nécessaire de recourir à un modèle à effets mixtes plus complexe mais plus général qu’une ANOVA (analyse de la variance) sur mesures répétées.
Références
- Declercq T. Forme simplifiée de restriction de sommeil comme traitement de l’insomnie en première ligne de soins ? MinervaF 2016;15(6):136-9.
- Falloon K, Elley CR, Fernando A 3rd, et al. Simplified sleep restriction for insomnia in general practice: a randomized controlled trial. Br J Gen Pract 2015;65:e508-15.
- Poelman T. Analyse des variables continues au moyen d’une ANCOVA. MinervaF 2014;13(8):103.
- Bland JM, Altman DG. Correlation, regression, and repeated data. BMJ 1994;308:896.
- Sedgwick P. One way analysis of variance. BMJ 2012;344:e2427.
- Petrie A, Sabin C. Medical statistics at a glance. John Wiley & Sons 2009 (3rd ed.).
Auteurs
Poelman T.
Vakgroep Volksgezondheid en Eerstelijnszorg, UGent
COI :
Michiels B.
Vakgroep Eerstelijns- en Interdisciplinaire Zorg, Centrum voor Huisartsgeneeskunde, Universiteit Antwerpen
COI :
Glossaire
Code
Ajoutez un commentaire
Commentaires