Revue d'Evidence-Based Medicine
Méta-analyse en réseau : comparaisons directes et indirectes
Formation médicale continue ~ Concepts et outils en EBM
| La rédaction consacre une rubrique ‘Formation médicale continue’ (FMC) à l’explicitation de concepts et outils en Evidence-Based Medicine (EBM). |
Les preuves les plus solides, les moins entachées de biais, proviennent d’études randomisées contrôlées. Les comparaisons entre médicaments utilisés pour une même indication doivent, pour être valides, rentrer dans ce moule. De nombreuses comparaisons ne sont malheureusement pas faites, ou du moins pas publiées. Des comparaisons indirectes peuvent-elles compenser l’absence ou compléter la rareté des comparaisons directes ? Est-il possible de sommer les données de comparaisons directes et indirectes - d’assembler des comparaisons mixtes - avec un niveau de fiabilité statistique suffisant (non biaisé) ? Les méta-analyses en réseau ont été conçues dans ce but. Quels principes fondamentaux doivent-elles suivre pour être valides ?
Comparaison directe et indirecte
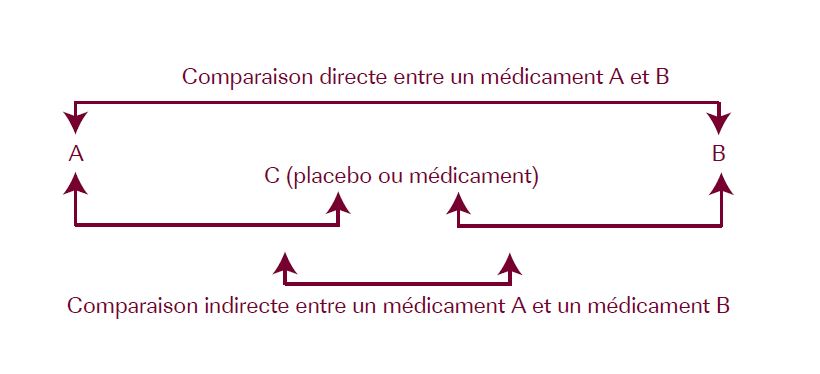
Une comparaison indirecte peut être faite de manière dite naïve : comparaison des résultats de deux études, de deux méta-analyses différentes, de résultats de bras d’études de recherches différentes. De telles comparaisons sont biaisées. Une comparaison indirecte peut être non biaisée si elle compare deux interventions elles-mêmes comparées à une même intervention (placebo ou médicament C dans notre exemple).
Des techniques plus élaborées sont également disponibles pour les comparaisons indirectes, intégrant la notion de distribution de probabilité du paramètre à estimer. Le but d’un tel processus est de tenter de prendre en compte toutes les probabilités. Elles ont recours à des analyses bayésiennes se basant sur les méthodes de Monte Carlo par chaînes de Markov mais avec des analyses numériques plus poussées que dans les modèles classiques. Une méthode de Monte Carlo, du nom du célèbre casino, est basée sur l’observation de la distribution d’une variable permettant de déterminer la valeur la plus probable. Un modèle de chaînes de Markov reprend différents états de santé avec les différentes transitions possibles entre ceux-ci, sur un cycle de temps précis, en fonction des traitements donnés. Une autre méthode utilisable est la classique méta-régression (modélisation de l’effet observé à l’aide de covariables).
Comparaison indirecte ajustée
Comme pour une méta-analyse d’études comparant un médicament A à un médicament B, une homogénéité (plus exactement une absence d’hétérogénéité) est nécessaire dans les méta-analyses comparant A et C et comparant B et C. Pour ajuster une comparaison indirecte, il faut ajouter à cette notion classique de méta-analyse de comparaisons directes, la nécessité d’une similarité entre toutes les études pour pouvoir comparer A et B en se servant de C comme comparateur. La similarité (similarity) porte sur un volet clinique (caractéristiques similaires des patients, des interventions, des contextes d’étude, de la durée de suivi, des critères de jugement) mais aussi sur un volet méthodologique (risque de biais dans les études) (1). Plusieurs auteurs insistent sur la nécessité de mieux évaluer encore les méthodes de comparaisons indirectes (2).
Comparaison mixte
D’autres méthodes existent qui, modélisant tous les traitements concurrents dans une même indication, combinent comparaisons directes et indirectes. Il s’agit de comparaisons mixtes ou méta-analyses en réseau. Ces méthodes se placent dans une approche bayésienne, et utilisent les techniques de Monte Carlo sur chaîne de Markov. Cette méthode requiert aussi de spécifier à l’avance certaines distributions des paramètres (distribution a priori).
Pour être valide, cette méthode doit concerner un réseau d’études avec homogénéité et similarité mais, en plus, avec cohérence (consistency) des données. Une incohérence des données est observée (Test I² de Higgins) si une différence existe entre les résultats des comparaisons directes et ceux des comparaisons indirectes. Dans les conditions où le médicament B a été évalué versus C placebo, le médicament A aurait donné le même risque relatif versus C. Mais le comparateur C pourrait aussi être, dans d’autres études, un comparateur actif. Il faut donc qu’il n’y ait pas d’incohérence suivant les différents chemins par lesquels la comparaison peut être faite entre A et B (3).
Ces différences peuvent être liées au hasard, à la non validité des comparaisons indirectes, à des biais dans les comparaisons directes ou à une hétérogénéité clinique (1).
Chacune des 3 notions précitées pour les comparaisons (homogénéité, similarité, cohérence) doit, dans l’ordre, être présente pour que la suivante acquière sa pertinence : homogénéité nécessaire pour toute sommation de résultats ; homogénéité et similarité nécessaire pour une comparaison indirecte ajustée ; homogénéité, similarité et cohérence nécessaires pour une comparaison mixte ou une sommation des résultats de comparaisons directes et indirectes.
Références
- Song F, Loke YK, Walsh T, et al. Methodological problems in the use of indirect comparisons for evaluating healthcare interventions: survey of published systematic reviews. BMJ 2009;338:b1147.
- Glenny AM, Altman DG, Song F, et al; International Stroke Trial Collaborative Group. Indirect comparisons of competing interventions. Health Technol Assess 2005;9:1-134.
- Cucherat M. Comparaisons indirectes et méta-analyse en réseau. http://www.spc.univ-lypn1.fr/polycop/sommaire2.htm (consulté le 17/05/2009).
Ajoutez un commentaire
Commentaires